Artykuł ten będzie inny niż poprzednie, nie będzie o programowaniu w języku Java z perspektywy młodszego programisty, programistki. Nie będzie on wykładem z matematyki, ale opisem mojego podejścia do próby zrozumienia pojęć i wzorów matematycznych. Pojęć i wzorów, które “dobrze znamy na pamięć” z lekcji matematyki, ale czy, aby na pewno dobrze je rozumiemy? Artykuł ten będzie moją próbą udokumentowania ścieżki, którą przeszedłem od korzenia kwadratu (pierwiastka kwadratowego), poprzez postęp geometryczny (pol.: ciąg, ang.: sequence), aż do “spotkania” Fibonacciego z Feynmanem.

Skąd w ogóle pomysł na naukę w inny sposób niż ten z zajęć szkolnych, czy też ten ze studiów? Po prostu uczenie się na pamięć pojęć i wzorów bez praktycznego zastosowania i dogłębnego zrozumienia tematu nigdy nie miało dla mnie sensu. Ucząc się nowego pojęcia, wzoru zawsze zadawałem sobie pytanie “Po co mi to? Do czego mogę, to wykorzystać?”. Ciekawym podejściem jest Technika Feynmana.

W podręczniku do matematyki dla liceów i techników z 2015 r., można znaleźć “praktyczne zastosowanie” ciągu geometrycznego na przykładzie “Lokaty pieniężne i kredyty bankowe”. Czy na prawdę trzeba było cały podrozdział poświęcić temu jak brać kredyty i obliczać lokaty? Od razu przypominają mi się moje lekcje “przedsiębiorczości”, gdzie wypełnialiśmy PITy, czyli formularze deklaracji podatkowych. Zarówno lokaty, kredyty oraz PITy opierają się na czymś wymyślonym przez człowiek i zmiennym w czasie. Potrzebowałem czegoś, co jest “od zawsze” w otaczającym nas świecie i można spróbować, to ubrać w pojęcia i wzory matematyczne.

Zdaję sobie sprawę, że na rynku wydawniczym jest cała masa książek, które lepiej lub gorzej próbują wytłumaczyć skomplikowane pojęcia i wzory matematyczne w sposób przystępny dla czytelników o różnym poziomie wiedzy. Na swojej drodze napotkałem poniższe książki, które podejmują próbę wyjaśnienia pojęć matematycznych w przystępny sposób:

Do powyższego wstępu dotyczącego samego sposobu uczenia się dodam jeszcze kwestię szybkiej dezaktualizacji, nieprawdziwości informacji, którą jesteśmy obecnie zalewani we współczesnym świecie. Dlatego postanowiłem, że moje źródła wiedzy muszą być “starsze niż 40 lat”, a wiedza w nich zawarta będzie dość niezmienna w czasie.

Natrafiłem na książkę Sacred Geometry: Philosophy and Practice – Robert Lawlor (data pierwszego wydania 1982 rok, 41 lat temu), pomyślałem, że, to coś dla mnie, będzie o jednym z działów matematyki – geometria – do tego w kontekście starożytnych cywilizacji.

“The thinkers of ancient Egypt, Greece and India recognized that numbers governed much of what they saw in their world and hence provided an approach to its divine creator.”

Opisując poniżej pojęcia matematyczne będę równolegle stosował polskie i angielskie określenia terminów matematycznych, gdyż moim zdaniem niektóre “tłumaczenia” pojęć gubią pierwotne znaczenie w języku polskim. Oczywiście, to moja subiektywna opinia, ale zawsze łatwiej było mi zrozumieć dane pojęcie matematyczne, kiedy poznałem jego anglojęzyczny odpowiednik dla języka polskiego.

Powyższa książka – Sacred Geometry – pozwoliła mi zrozumieć pojęcie pierwiastka kwadratowego bez używania jakiegokolwiek wzoru matematycznego. Cała wiedza dotycząca pierwiastka kwadratowego oraz ciągu geometrycznego została pokazana poprzez rysowanie połączonych – za pomocą przekątnej – ze sobą kwadratów, z których pierwszy ma boki o długości 1 cm.

Obliczając na kalkulatorze \sqrt{2} otrzymujemy wynik 1,414213562. Tyle również wynosi przekątna kwadratu, którego bok ma długość 1 cm.

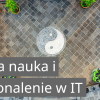
Poniżej rysunki prezentujące ciąg geometryczny wykorzystujący pierwiastek kwadratowy (ang. square root). Rysunki wykonane zgodnie z instrukcjami z książki Sacred Geometry.

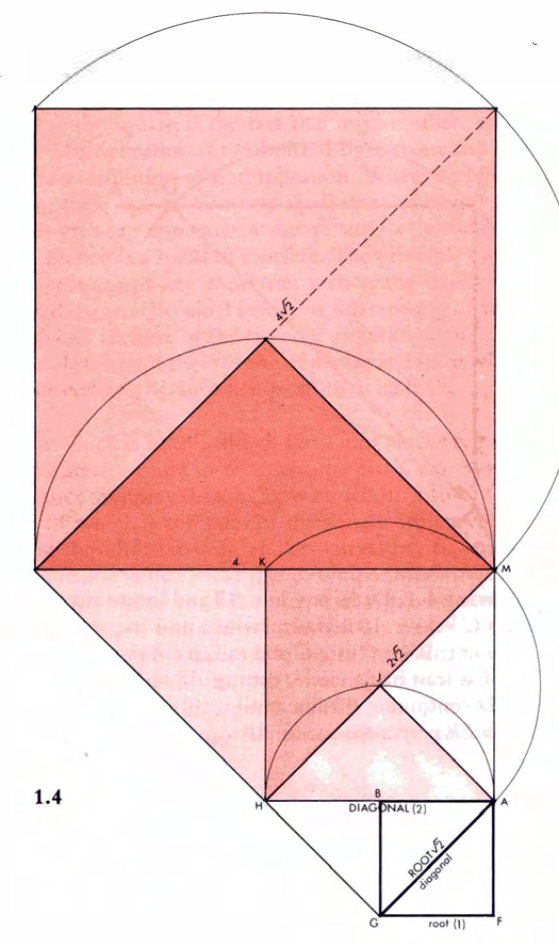
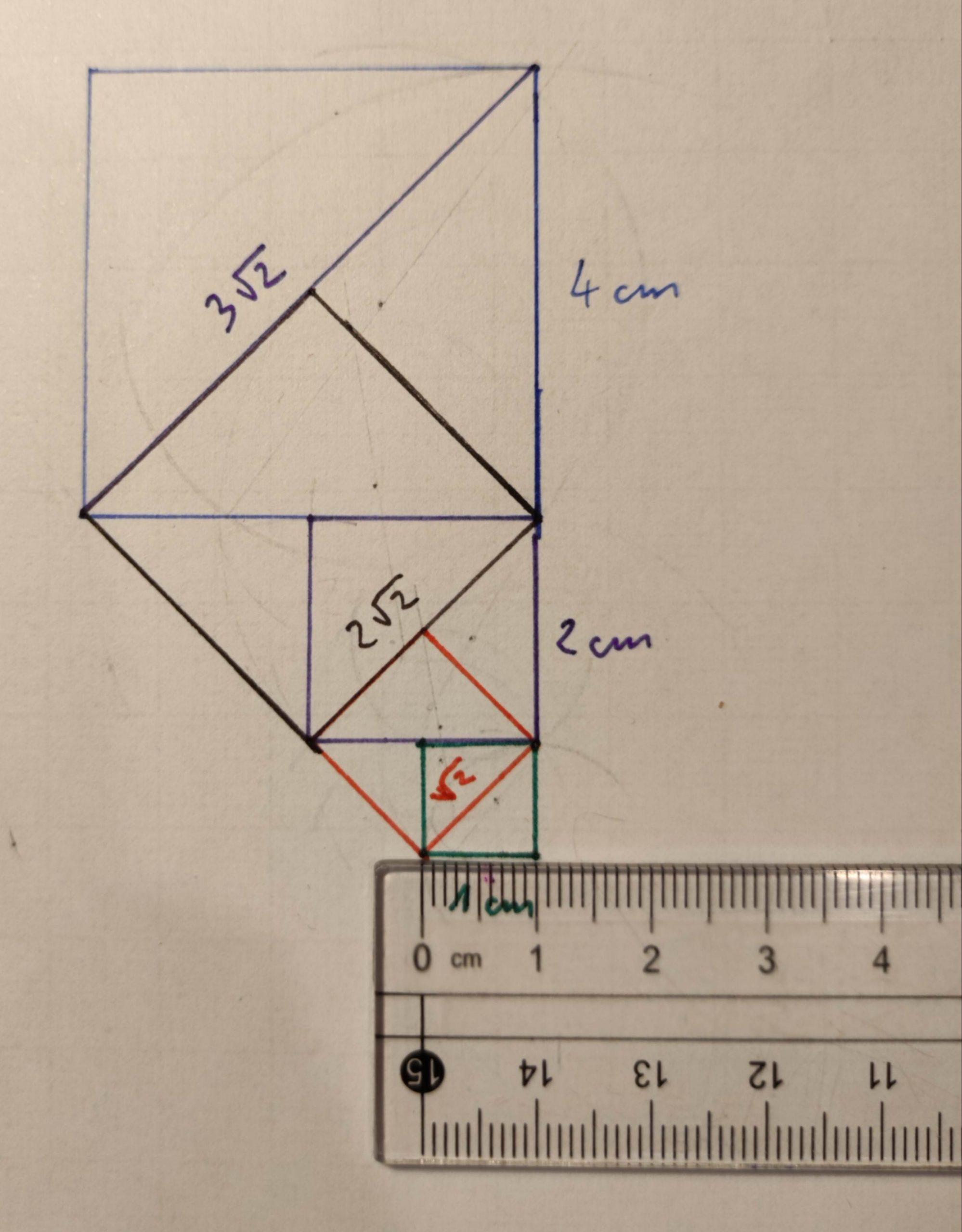
Rysunek z ksiazki Sacred Geometry: Philosophy and Practice, str. 26, rys. 1.4
Moj odreczny rysunek zgodny z instrukcjami z Sacred Geometry: Philosophy and Practice, str. 25-26, rys. 1.1. – 1.4.

Podstawą kolejnego kwadratu staje się przekątna poprzedniego – w tym momencie znalazłem wyjaśnienie, pochodzenie pojęcia “square root” – w wolnym tłumaczeniu korzeń kwadratu. Postępując (ang. progression) kolejno i rysując nowe kwadraty, których podstawą są przekątne poprzednich kwadratów otrzymujemy ciąg (ang. sequence) geometryczny (ang. geometric progression). W tym miejscu znajduje się wyjaśnienie jednej z części “tajemniczego” tytułu mojego artykułu.

Powyższa galeria rysunków zawiera instrukcje z ksiązki Sacred Geometry: Philosophy and Practice, str. 25-26, rys. 1.1. – 1.4., które pozwolą na samodzielne narysowanie korzenia kwadratu (ang. square root, pol. pierwiastek kwadratowy) w kontekście ciągu geometrycznego (ang. geometric progression).

Poniższe obrazy pokazują jak wyglądały narzędzia – “do geometrii” – używane przez starożytnych oraz współczesne odpowiedniki narzędzi, których sam używam.

Sacred Geometry Tools - Ancient
Sacred Geometry Tools – starozytne narzedzia “do geometrii”.
Sacred Geometry Tools - Contemporary
Moje wspolczesne odpowiedniki narzedzi do geometrii.

Dodatkowo w trakcie pisania tego artykułu uczyłem się w praktyce jak zapisywać wzory matematyczne z wykorzystaniem LaTeX. “LaTeX jest szeroko stosowany w środowisku akademickim do komunikacji i publikacji dokumentów naukowych z wielu dziedzin, w tym matematyki, informatyki […]. Odgrywa również znaczącą rolę w przygotowywaniu i publikowaniu książek i artykułów […].”.

Tak wygląda wzór matematyczny przed przetworzeniem przez LaTeX – a_{n}=a \cdot r^{n-1} – tak wygląda po przetworzeniu a_{n}=a \cdot r^{n-1}.

Pokrzepiony i zainspirowany “odkryciem znaczenia” pierwiastka kwadratowego zabrałem się za zgłębianie praktycznycznego zastosowania ciągu geometrycznego (ang. geometric progression). Ciąg nazywamy geometrycznym, jeśli stosunek między kolejnymi wyrazami jest stały.

Pamiętałem dwa wzory dla ciągu geometrycznego:

Wzór na n-ty wyraz ciągu geometrycznego – postać jawna (ang. closed formula):

a_{n}=a \cdot r^{n-1}

Wzór na n-ty wyraz ciągu geometrycznego – postać rekurencyjna (ang. recursive formula):

a_{n}=a_{n-1} \cdot r

Przykład ciągu geometrycznego:

3, 6, 12, 24, \dots

Sprawdzę czy mam do czynienia z ciągiem geometrycznym dzieląc każdy wyraz przez jego poprzedni wyraz: 6/3 = 2, 12/6 = 2, 24/12 = 2. Zakładając, że ten stosunek jest stały, znalazłem r = 2 – ciąg nazywamy geometrycznym, jeśli stosunek między kolejnymi wyrazami jest stały.

W podręcznikach do matematyki i na polskojęzycznej Wikipedii zamiast r używane jest q, ale dla mnie łatwiej było zrozumieć wersję równania z r, bo jest, to pierwsza litera od angielskiego wyrazu ratio – pol. stosunek, współczynnik.

Wzór na n-ty wyraz – postać jawna.

a_{n}=a \cdot r^{n-1}

Podstawiam r = 2.

a_{n}=3 \cdot 2^{n-1}

Obliczam dla kolejnych wyrazów ciągu.

a_{1}=3
a_{2}=3 \cdot 2^{2-1}=3 \cdot 2^{1} = 3 \cdot 2 = 6
a_{3}=3 \cdot 2^{3-1}=3 \cdot 2^{2} = 3 \cdot 4 = 12
a_{4}=3 \cdot 2^{4-1}=3 \cdot 2^{3} = 3 \cdot 8 = 24
a_{5}=3 \cdot 2^{5-1}=3 \cdot 2^{4} = 3 \cdot 16 = 48

Wzór na n-ty wyraz – postać rekurencyjna.

a_{n}=a_{n-1} \cdot r

Podstawiam r = 2.

a_{n}=a_{n-1} \cdot 2

Obliczam dla kolejnych wyrazów ciągu.

a_{1}=3
a_{2}=a_{2-1} \cdot 2 = a_{1} \cdot 2 = 3 \cdot 2 = 6
a_{3}=a_{3-1} \cdot 2 = a_{2} \cdot 2 = 6 \cdot 2 = 12
a_{4}=a_{4-1} \cdot 2 = a_{3} \cdot 2 = 12 \cdot 2 = 24
a_{5}=a_{5-1} \cdot 2 = a_{4} \cdot 2 = 24 \cdot 2 = 48

Poniżej zapis wzoru na n-ty wyraz ciągu geometrycznego w postaci jawnej – kod języka Java. Używam pętli for do obliczania kolejnych wyrazów w ciągu geometrycznym.

static int geometricProgressionLoop(int a_n, int r, int terms) {
    int result = 0;
    for (int n = 0; n < terms; n++) {
        result = (int) (a_n * Math.pow(r, n));
    }
    return result;
}

Poniżej zapis wzoru na n-ty wyraz ciągu geometrycznego w postaci rekurencyjnej – kod języka Java. Metoda geometricProgressionRecursive() wywołuje samą siebie do obliczania kolejnych wyrazów w ciągu geometrycznym.

static int geometricProgressionRecursive(int a_n, int r, int terms) {
    if (a_n == terms) return 1;
    return a_n * r * geometricProgressionRecursive(a_n + 1, r, terms);
}

Poniżej przykłady praktycznego zastosowania ciągu geometrycznego:

  • Obliczanie uzyskanych odsetek,
  • Obliczenie kwoty na naszym koncie oszczędnościowym,
  • Obliczanie wielkości wykładniczego wzrostu populacji, na przykład bakterii na szalce Petriego,
  • Skończony ciąg geometryczny jest przykładem odbijającej się piłki. Wysokość piłki zmniejsza się o połowę przy każdym odbiciu.

Poniżej najbardziej znany przykład użycia rekurencji, czyli ciąg Fibonacciego. Kod źródłowy w języku Java oraz Python. 

int fibonacci(int n) {
    if (n < 2) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}
def fibonacci(n):
    if n < 2:
        return n
    return fibonacci(n - 1) + fibonacci(n - 2)

Osoby początkujące mogą skorzystać z narzędzi online, które przedstawiają w formie graficznej – wizualizują – działania algorytmów:

Tym samym uzyskałem obiecane w tytule artykułu spotkanie Fibonacciego z Feynmanem.

Podejmowałem już różne próby powtarzania i utrwalania wiedzy zdobytej w szkole, ale zawsze brakowało mi, tego praktycznego i namacalnego zastosowania pojęć i wzorów matematycznych. Na dalszych etapach nauki zapewne spotkam się z abstrakcyjnymi pojęciami i wzorami, które nie mają odzwierciedlenia w świecie rzeczywistym, wtedy zastanowię się nad tym czy matematyka, aby nie jest tworem ludzkiego umysłu i jest oderwana od rzeczywistości. Feynman twierdził, że matematyka nie jest nauką – https://www.goodreads.com/quotes/1459603-mathematics-is-not-a-science-from-our-point-of-view:

Richard P. Feynman, The Feynman Lectures on Physics Vol 1

“Mathematics is not a science from our point of view, in the sense that it is not a natural science. The test of its validity is not experiment.”.

Patrząc na przykład z korzeniem kwadratu (ang. square root) znalezionego w książce “Sacred Geometry…” wraca moja nadzieja, że matematyka może być próbą znalezienia sposobu na zapisanie wzorami otaczającego nas świata. Tymczasem ja szukam innych źródeł – niż matematyka – opisujących otaczający nas świat.

Podsumowując, artykuł ten pozwolił mi zastosować w praktyce: technikę Feynmana, zapis wzorów matematycznych z wykorzystaniem LaTeX, kod języka programowania w odniesieniu do ciągu geometrycznego (ang. geometric progression). Wiedzę, którą tu przedstawiłem nie przyswoiłem w “jeden dzień”, jest ona wynikiem “kompilacji” wiedzy z różnych źródeł z celowym pominięciem – “dobrze przeszkolonego pracownik informacji turystycznej” – sztucznej inteligencji. Jestem ciekawy czy, taka forma artykułu się spodoba?

Kontakt
Mentoring – rezerwuj termin

Zdjęcie autorstwa Yaroslav Shuraev z Pexels.

795