This article will be different than the previous ones, it will not be about programming in Java from the perspective of a junior programmer. It will not be a lecture on mathematics, but a description of my approach to trying to understand mathematical concepts and formulas. Concepts and formulas that we "know well by heart" from mathematics lessons, but do we really understand them well? This article will be my attempt to document the path I followed from the root of the square (square root), through geometric progression, and sequence, to the "meeting" of Fibonacci and Feynman.

Where did the idea of learning in a different way than from school or university come from? Simply memorizing concepts and formulas without practical application and a thorough understanding of the topic has never made sense to me. When learning a new concept or pattern, I always asked myself, "Why do I need this? What can I use it for?” An interesting approach is Feynman Technique.

In a mathematics textbook for high schools and technical schools from 2015, you can find a "practical application" of a geometric sequence on the example of "Money deposits and bank loans". Was it really necessary to devote an entire subchapter to how to take out loans and calculate deposits? I immediately remember my "entrepreneurship" lessons, where we filled out PITs, i.e. tax declaration forms. Both deposits, loans and PITs are based on something invented by humans and change over time. I needed something that has "always been" in the world around us and you can try to put it into mathematical concepts and formulas.

I am aware that there are a lot of books on the publishing market that, better or worse, try to explain complex mathematical concepts and formulas in a way that is accessible to readers with different levels of knowledge. On my way, I came across the following books that attempt to explain mathematical concepts in an accessible way:

To the above introduction regarding the way of learning itself, I will add the issue of rapid obsolescence and untrue information that we are currently flooded with in the modern world. Therefore, I decided that my sources of knowledge must be "older than 40 years" and the knowledge contained in them will be quite constant over time.

I came across a book Sacred Geometry: Philosophy and Practice – Robert Lawlor (first published 1982, 41 years ago), I thought it was something for me, it will be about one of the branches of mathematics - geometry - and in the context of ancient civilizations.

„The thinkers of ancient Egypt, Greece and India recognized that numbers governed much of what they saw in their world and hence provided an approach to its divine creator.”

When describing mathematical concepts below, I will use Polish and English definitions of mathematical terms in parallel, because in my opinion some "translations" of concepts lose their original meaning in Polish. Of course, this is my subjective opinion, but it was always easier for me to understand the data mathematical concept when I learned its English equivalent in Polish.

The above book - Sacred Geometry - allowed me to understand the concept of square root without using any mathematical formula. All knowledge about square roots and geometric sequences was demonstrated by drawing squares connected - by a diagonal - with the first square having sides of 1 cm.

Calculating on a calculator \sqrt{2} we get the result 1.414213562. This is also the diagonal of a square whose sides are 1 cm long.

Below are drawings presenting a geometric sequence using a square root. Drawings made according to instructions from the book Sacred Geometry.

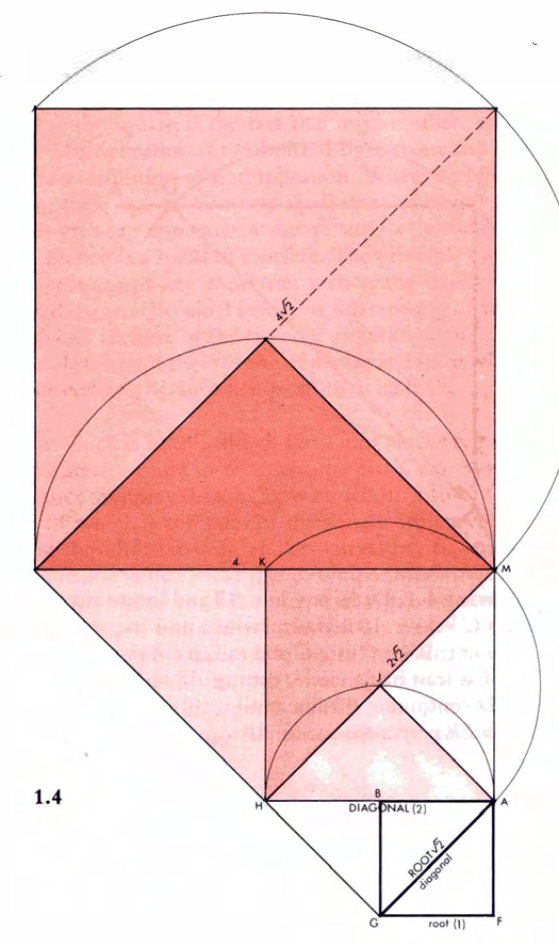
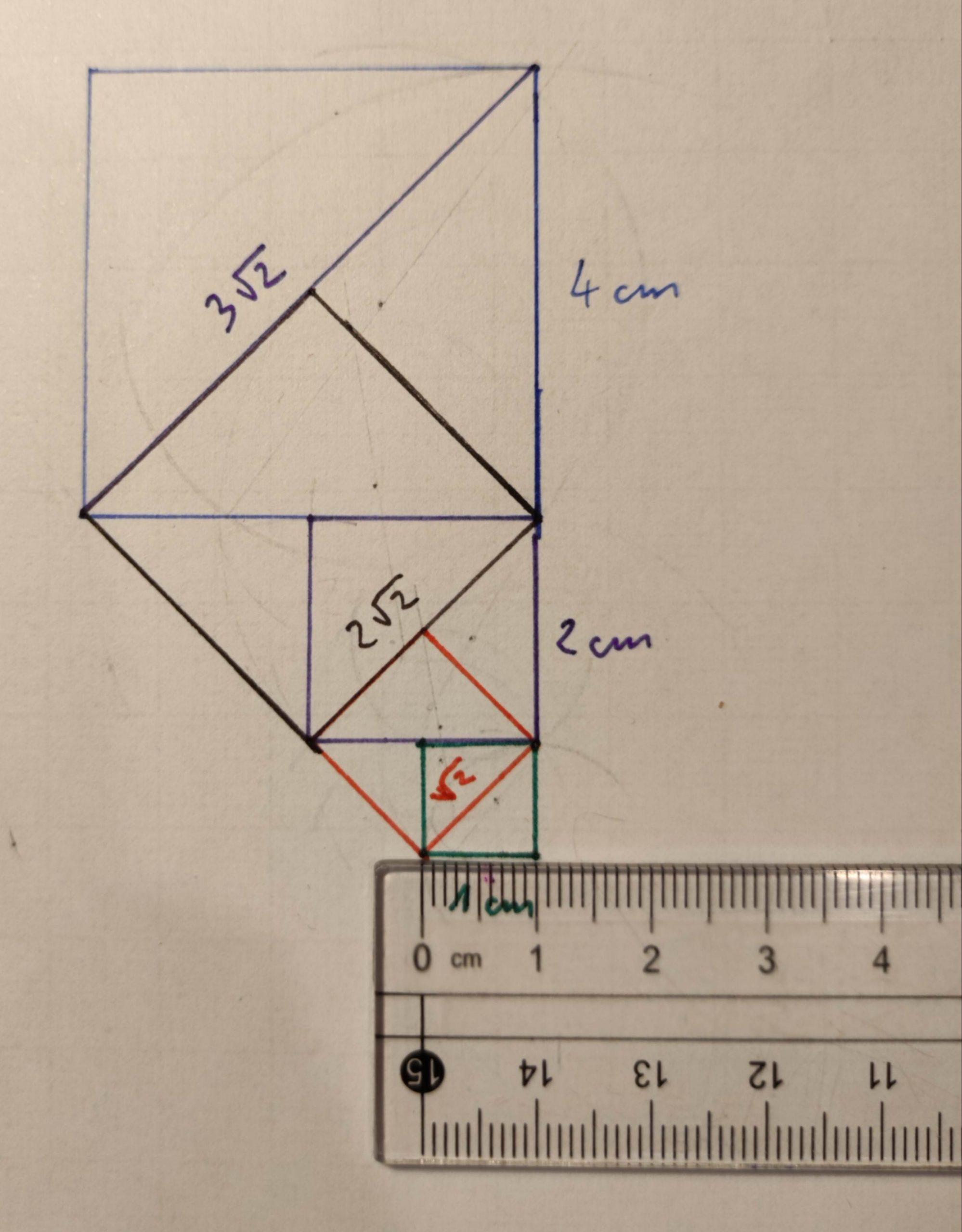
Drawing from the book Sacred Geometry: Philosophy and Practice, page 26, figure 1.4
My hand drawing according to the instructions from Sacred Geometry: Philosophy and Practice, pp. 25-26, Fig. 1.1. – 1.4.

The basis of the next square becomes the diagonal of the previous one - at this point I found an explanation, the origin of the concept of "square root" - loosely translated, the root of a square. By progressively drawing new squares based on the diagonals of the previous squares, we obtain a geometric sequence. Here is an explanation of one part of the "mysterious" title of my article.

The gallery of drawings above contains instructions from the book Sacred Geometry: Philosophy and Practice, pp. 25-26, figure 1.1. – 1.4., which will allow you to independently draw a square root in the context of a geometric progression.

The images below show what the "geometry" tools used by the ancients looked like and the modern equivalents of the tools I use myself.

Sacred Geometry Tools - Ancient
Sacred Geometry Tools – ancient “geometry” tools.
Sacred Geometry Tools - Contemporary
My modern equivalents of geometry tools.

Additionally, while writing this article, I learned in practice how to write mathematical formulas using LaTeX. “LaTeX is widely used in academia for communicating and publishing scientific documents in many fields, including mathematics, computer science […]. It also plays a significant role in preparing and publishing books and articles [...].

This is what the mathematical formula looks like before processing by LaTeX – a_{n}=a \cdot r^{n-1} – this is what it looks like after processing a_{n}=a \cdot r^{n-1}.

Encouraged and inspired by the "discovery of the meaning" of the square root, I set about exploring the practical application of geometric progression. A sequence is called geometric if the ratio between successive terms is constant.

I remembered two formulas for a geometric sequence:

Formula for the n-th term of a geometric sequence – closed formula:

a_{n}=a \cdot r^{n-1}

Formula for the n-th term of a geometric sequence – recursive formula:

a_{n}=a_{n-1} \cdot r

Example of a geometric sequence:

3, 6, 12, 24, \dots

I will check whether I am dealing with a geometric sequence by dividing each term by its previous term: 6/3 = 2, 12/6 = 2, 24/12 = 2. Assuming that this ratio is constant, I found r = 2 - a sequence is called geometric if the ratio between successive terms is constant.

In mathematics textbooks and in Polish-language Wikipedia instead of r q is used, but for me it was easier to understand the r version of the equation, because it is the first letter of the English word ratio - Polish. ratio, ratio.

Formula for nth word – explicit form.

a_{n}=a \cdot r^{n-1}

I substitute r = 2.

a_{n}=3 \cdot 2^{n-1}

I calculate for the next terms of the sequence.

a_{1}=3
a_{2}=3 \cdot 2^{2-1}=3 \cdot 2^{1} = 3 \cdot 2 = 6
a_{3}=3 \cdot 2^{3-1}=3 \cdot 2^{2} = 3 \cdot 4 = 12
a_{4}=3 \cdot 2^{4-1}=3 \cdot 2^{3} = 3 \cdot 8 = 24
a_{5}=3 \cdot 2^{5-1}=3 \cdot 2^{4} = 3 \cdot 16 = 48

The formula for the nth word – recursive form.

a_{n}=a_{n-1} \cdot r

I substitute r = 2.

a_{n}=a_{n-1} \cdot 2

I calculate for the next terms of the sequence.

a_{1}=3
a_{2}=a_{2-1} \cdot 2 = a_{1} \cdot 2 = 3 \cdot 2 = 6
a_{3}=a_{3-1} \cdot 2 = a_{2} \cdot 2 = 6 \cdot 2 = 12
a_{4}=a_{4-1} \cdot 2 = a_{3} \cdot 2 = 12 \cdot 2 = 24
a_{5}=a_{5-1} \cdot 2 = a_{4} \cdot 2 = 24 \cdot 2 = 48

Below is the formula for the n-th term of a geometric sequence in explicit form - Java code. I use a for loop to evaluate subsequent terms in a geometric sequence.

static int geometricProgressionLoop(int a_n, int r, int terms) {
    int result = 0;
    for (int n = 0; n < terms; n++) {
        result = (int) (a_n * Math.pow(r, n));
    }
    return result;
}

Below is the formula for the n-th term of a geometric sequence in recursive form - Java code. The geometricProgressionRecursive() method calls itself to calculate subsequent terms in the geometric sequence.

static int geometricProgressionRecursive(int a_n, int r, int terms) {
    if (a_n == terms) return 1;
    return a_n * r * geometricProgressionRecursive(a_n + 1, r, terms);
}

Below are examples of practical applications of a geometric sequence:

  • Calculation of interest earned,
  • Calculating the amount in our savings account,
  • Calculating the amount of exponential population growth, for example bacteria in a Petri dish,
  • A finite geometric sequence is an example of a bouncing ball. The height of the ball is halved with each bounce.

Below is the most famous example of using recursion, i.e. Fibonacci sequence. Source code in Java and Python.

int fibonacci(int n) {
    if (n < 2) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}
def fibonacci(n):
    if n < 2:
        return n
    return fibonacci(n - 1) + fibonacci(n - 2)

Beginners can use online tools that graphically present - visualize - the operation of algorithms:

Thus, I achieved the meeting between Fibonacci and Feynman promised in the title of the article.

I have already made various attempts to repeat and consolidate the knowledge acquired at school, but I always missed the practical and tangible application of mathematical concepts and formulas. At further stages of learning, I will probably encounter abstract concepts and patterns that have no reflection in the real world, then I will consider whether mathematics is not a creation of the human mind and is detached from reality. Feynman claimed that mathematics is not a science – https://www.goodreads.com/quotes/1459603-mathematics-is-not-a-science-from-our-point -of-view:

Richard P. Feynman, The Feynman Lectures on Physics Vol 1

“Mathematics is not a science from our point of view, in the sense that it is not a natural science. The test of its validity is not experiment.”.

Looking at the example of the square root found in the book "Sacred Geometry..." my hope returns that mathematics can be an attempt to find a way to write down the world around us with patterns. Meanwhile, I am looking for sources other than mathematics that describe the world around us.

To sum up, this article allowed me to put into practice: Feynman's technique, writing mathematical formulas using LaTeX, programming language code in relation to geometric progression. The knowledge I presented here was not acquired in "one day", it is the result of a "compilation" of knowledge from various sources with the intentional omission of - "a well-trained tourist information employee" - artificial intelligence. I wonder if you will like this form of the article?

Contact
Mentoring - book an appointment

Zdjęcie autorstwa Yaroslav Shuraev z Pexels.

621